Энергетические уровни в разрешенных зонах полупроводников распределены неравномерно. В любой энергетической зоне энергетические уровни характеризуются определенной плотностью Ф(W), т.е. числом уровней, отнесенным к единице энергии и единице объема:
![]() , (1.3)
, (1.3)
где А -некоторый коэффициент;
W - текущее значение энергии;
WГР - граничное значение энергии.
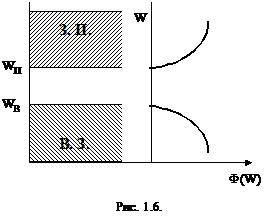
Вблизи "дна" и "потолка" каждой из зон плотность уровней распределяется так, как показано на рис.1.6.
Вероятность нахождения электрона при данной температуре на уровне с энергией W определяется функцией Ферми:
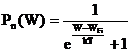 , (1.4)
, (1.4)
где k - постоянная Больцмана, k = 1,38×10-23Дж/град = 0,86×10-4эВ/град;
WFi - энергия, соответствующая уровню Ферми;
Т - абсолютная температура.
При Т = 0К функция Рn(W) принимает следующие значения:
если W>WFi, то Pn(W) = 0;
если W<WFi, то Pn(W) = 1.
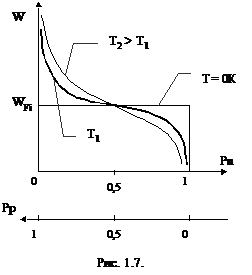
Т.о. при абсолютном нуле все уровни ниже уровня Ферми полностью заняты, а уровни выше уровня Ферми полностью свободны, т.е. функция Pn(W) имеет ступенчатый характер. При повышении температуры функция Pn(W) сглаживается и вероятность появления электрона в зоне проводимости становится отличной от нуля (рис.1.7.). Одновременно вероятность появления дырки в валентной зоне тоже становится отличной от нуля. Вероятность нахождения дырки при данной температуре на уровне с энергией W определяется функцией:
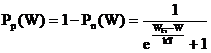 , (1.5)
, (1.5)
Понятие уровня Ферми имеет достаточно сложный физический смысл. Его можно рассматривать, во-первых, как максимально возможное значение энергии электрона при абсолютном нуле температуры, и , во-вторых, как энергетический уровень, вероятность заполнения которго равна 0,5.
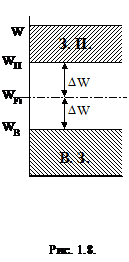
Т.к. в чистом полупроводнике концентрация дырок равна концентрации электронов, то уровень Ферми находится строго посередине запрещенной зоны (рис.1.8):
![]() . (1.6)
. (1.6)
На этом рисунке
![]() . (1.7)
. (1.7)
Полупроводники, у которых DW ≥ 3kT, называют невырожденными. Если DW < 3kT, то полупроводник называют вырожденным. Вырожденные полупроводники получаются при высоких температурах или при большой концентрации носителей зарядов. Для невырожденных полупроводников можно найти выражения для концентрации носителей зарядов:
![]() , (1.8)
, (1.8)
![]() , (1.9)
, (1.9)
где Аnи Ар - универсальные константы и зависят от материала полупроводника.
Т.к. концентрация зарядов в разрешенных зонах экспоненциально зависит от температуры, то и электропроводность соответствующих полупроводников также экспоненциально зависит от температуры.
При комнатной температуре (Т = 300К) концентрация носителей зарядов для германия (Ge) n = p ≈ 1013см -3, для кремния (Si) n = p ≈ 1010см –3. Для сравнения: концентрация атомов в металлах при этой температуре N ≈ 1022см –3. Т.о. можно сделать вывод, что при комнатной температуре чистые полупроводники практически являются диэлектриками.