Любую нелинейную функцию у(х) с заданной степенью точности можно аппроксимировать ломаной линией, которая может быть сформирована совокупностью ломаных лучей (рис. 5.1).
Рис. 5.1
Таким образом, задача сводится к построению универсальной схемы, позволяющей менять точки перегиба и передаточные характеристики (рис.1.2, а).
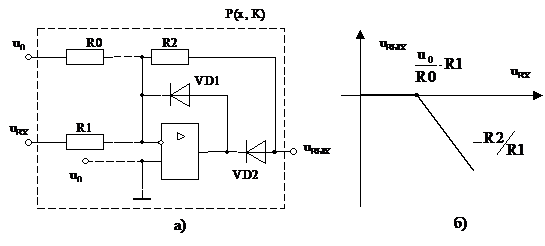
Рис. 5.2
Обозначим:
. (5.1)
Если 
, то выходное напряжение 
.
Т.е. при условии, что:
(5.2)
или 
(5.3)
При 
выходное напряжение будет uВЫХ < 0. Таким образом, положение точки перегиба может корректироваться.
. (5.4)
Коэффициент наклона:
. (5.5)
Точку перегиба (х) и наклон (коэффициент К) можно регулировать независимо, меняя R0 или R2 (рис.1.2, б).
На рис.1.3 представлен кусочно-линейный аппроксиматор из трех звеньев Рi(хi, Кi).
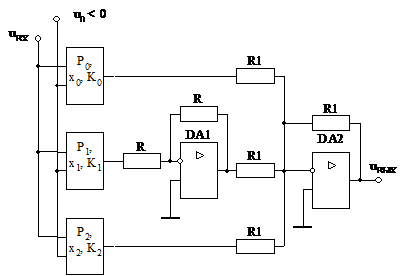
Рис. 5.3
При построении кусочно-линейных аппроксиматоров из большого количества звеньев суммирующие ОУ DA1 и DA2 делаются многовходовыми; выходы блоков, сигналы которых должны на выходе иметь положительный коэффициент, подключаются к ОУ DA2, а выходы блоков, сигналы которых должны на выходе иметь отрицательный коэффициент, подключаются к ОУ DA1.
Дополнительное управление коэффициентами передачи отдельных блоков может осуществляться выбором коэффициентов передачи сумматоров по каждому входу суммирования.
При проектировании кусочно-линейного аппроксиматора необходимо проверить, чтобы ни один выход ОУ не попадал в насыщение во всем диапазоне допустимого изменения входного сигнала.