В качестве хронирующего напряжения можно брать напряжение на конденсатора или в точке А (рис. 1.71).
В данном режиме работы состояние ЛЭ следующее: DD1 - в состоянии логической единицы, т.е. UВЫХ1 = U1; DD2 - в состоянии логического нуля, т.е. UВЫХ2 = U0. При отсутствии входных сигналов верхние свободные входы ЛЭ имеют нулевой потенциал.
Исходное состояние схемы: выбираем R1 и Е такими, чтобы DD1 находился в состоянии логической единицы; на входе DD2 напряжение е2 = 1 (см. временную диаграмму на рис. 1.73).
В данном режиме работы входной сигнал подается на вход второго ЛЭ е2. Если подается сигнал е2, соответствующий логическому нулю, то такой входной сигнал приводит к переключению логических элементов, т.е. к увеличению UВЫХ2, UA, UВХ и уменьшению UВЫХ1 до логического нуля.
Временные диаграммы для данного режима работы мультивибратора представлены на рис. 1.73.
С момента времени t0 конденсатор С начинает заряжаться по цепи "выход DD2 – С – R2 – R1 – E – общая шина" и частично через входное сопротивление DD1. Хронирующее напряжение UA и напряжение на входе DD1 начинают экспоненциально уменьшаться.
В момент времени t = t1 напряжение на входе DD1 достигает порогового значения, и оба ЛЭ попадают в активную область (участок 3' – 4' на рис. 1.72), замыкается цепочка ПОС с петлевым коэффициентом усиления, большим единицы, т.е. в схеме возникает регенеративный процесс, в результате которого ЛЭ возвращаются в исходное состояние. При этом диод VD открывается, т.е. напряжение на входе DD1 UВХ = UD = -е0. После этого начинается процесс восстановления напряжения на конденсаторе, который состоит из двух этапов:
1) tВ' = t2 – t1; на этом этапе диод VDоткрыт;
2) tВ" = t3 – t2; на этом этапе диод VDзакрыт.
Чтобы обеспечить исходное состояние схемы, нужно выбрать E и R1, выбрать рабочую точку на участке 1 – 2 входной характеристики (рис. 1.72).
Уравнение входной характеристики на участке 1 – 2:
![]() , (1.29)
, (1.29)
где rВХ - входное сопротивление ЛЭ; при входном напряжении, меньшем порогового значения (UВХ < UПОР), входное сопротивление:
![]() , (1.30)
, (1.30)
где еЭ0 - падение напряжения на открытом эмиттерном переходе многоэмиттерного транзистора.
Из принципиальной схемы мультивибратора следует, что:
![]() . (1.31)
. (1.31)
Это уравнение справедливо для статического режима.
Прямые I, IIна рис. 1.72. построены для Е = 0; прямая IIIпостроена в соответствии с (1.31) для какого-то значения Е. Точка пересечения входной характеристики с нагрузочной прямой (1.31) определяет начальное состояние ЛЭ.
При увеличении R1 рабочая точка будет смещаться по входной характеристике от точки 1 к точке 2. Точка 2 определяет максимальное значение сопротивления R1 для рассматриваемого режима работы. Чтобы найти входное напряжение, соответствующее рабочей точке, нужно совместно решить уравнения (1.30) и (1.31) при Е = 0. В результате решения получаем:
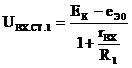 . (1.32)
. (1.32)
Из уравнения (1.32) можно найти максимальное значение сопротивления R1 в точке 2. Обозначив через UВХ2 напряжение, соответствующее точке 2, получим:
![]() . (1.33)
. (1.33)
Определим длительность генерируемого схемой импульса.
Длительность временно устойчивого состояния - это интервал времени t0 – t1 = t, на котором происходит процесс заряда конденсатора. Точно определить величину t не удается из-за нелинейности входной характеристики. Учитывая малое значение входного тока, соответствующего логической единице, можно положить IВХ1 = 0. На этом интервале диод VD закрыт, поэтому можно пренебречь его сопротивлением, т.е. riD = ¥. Тогда схема заряда конденсатора может быть представлена как на рис. 1.74.
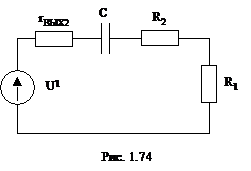
Учитывая экспоненциальный характер переходного процесса в схеме, запишем в общем виде выражение для длительности t:
![]() , (1.34)
, (1.34)
где Т1 = С×(rВЫХ2 + R2 + R1) есть постоянная времени контура. Если не учитывать падение напряжения на открытом диоде VD, то UВХ(¥) = 0. В формуле (1.34) UВХ(t1) = UПОР = 1,4 ¸1,6 В; UВХ(0) = UВХ.СТ.1 + (U1 – U0)×R1/(rВЫХ + R2 + R1).
Время восстановления - это интервал t1 – t3. На этом интервале DD1 находится в состоянии логического нуля, поэтому можно принять rВЫХ2 = 0. Диод VD открыт. Учитывая малую величину интервала tВ', можно принять за время восстановления:
tВ @ tВ" @ C×(R2 + R1||rВХ1)×КВОССТ. (1.35)
На интервале tВ" диод VD закрыт, и коэффициент восстановления:
КВОССТ = –ln(1 – КЗ), (1.36)
где КЗ - коэффициент затухания экспоненты.
Приняв КЗ = 0,8, получим КВОССТ = 1,6.